En funksjon av to variabler kan plottes på flere måter:
1. Graf: 3D plott med en graf som består av alle punkt der $z = f(x,y)$
2. Nivåkurver: 2D plott med kurver for forskjellige $z$-verdier
3. Snitt: 2D plott for en $x$- eller $y$-verdi
+ Kort video
+ Eksempel 1: $f(x,y) = x + y$
+ To videoer
Nivåkurver:
Snitt:
+ Grafen til $f(x,y) = x + y$
Grafen til $f(x,y)$ består av alle punkt $(x,y,z)$ som tilfredsstiller $f(x,y) = z$:
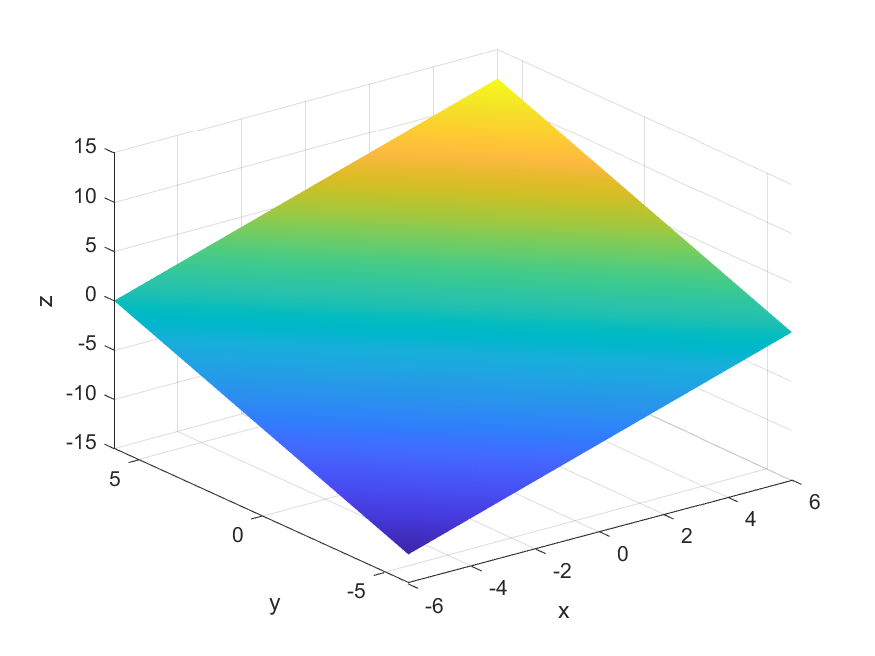
Eksempler på punkt på grafen:
- $(x,y,z) = (5,0,5)$ fordi $f(5,0) = 5 + 0 = 5$
- $(x,y,z) = (2,3,5)$ fordi $f(5,0) = 2 + 3 = 5$
- $(x,y,z) = (6,-1,5)$ fordi $f(5,0) = 6 + (-1) = 5$
+ Nivåkurver til $f(x,y) = x + y$
Nivåkurvene til $f(x,y)$ er kurver der $f(x,y)$ er konstant. Her er nivåkurvene $f(x,y) = k$ for noen valg av $k$:
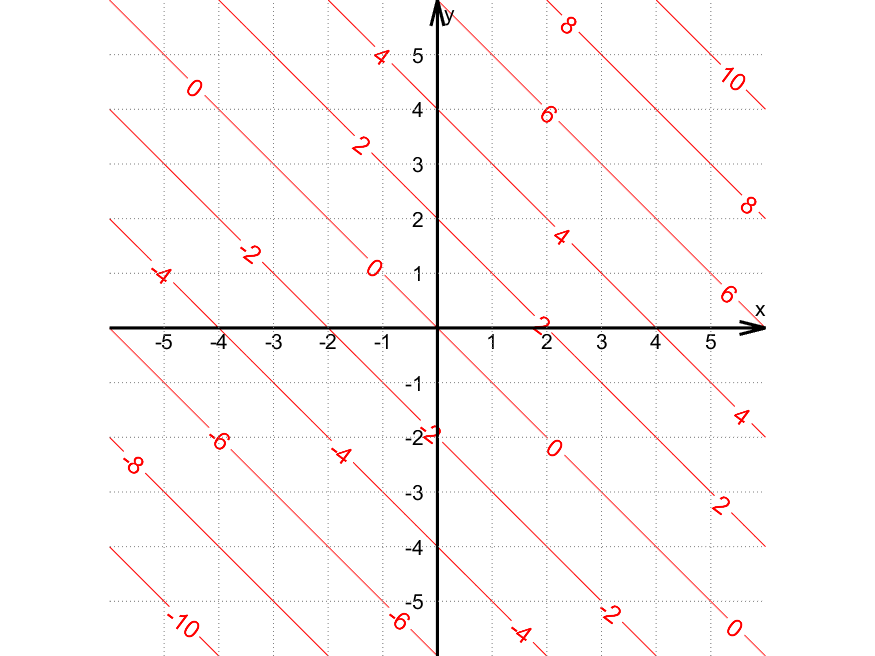
Eksempler på punkt på kurven for $k=\textcolor{red}{4}$:
- $(x,y) = (4,0)$ fordi $f(4,0) = 4 + 0 = \textcolor{red}{4}$
- $(x,y) = (2,2)$ fordi $f(2,2) = 2 + 2 = \textcolor{red}{4}$
- $(x,y) = (-1,5)$ fordi $f(-1,5) = -1 + 5 = \textcolor{red}{4}$
+ Snitt til $f(x,y) = x + y$
Et snitt kan tegnes for akkurat den $x$ eller $y$ verdien man ønsker.
Her er to snittet for $y = 0$, dvs. når $z = f(x,0) = x + 0$:

Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{0})$ fordi $z = f(\textcolor{red}{0},0) = \textcolor{red}{0} + 0 = \textcolor{blue}{0}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{2})$ fordi $z = f(\textcolor{red}{2},0) = \textcolor{red}{2} + 0 + \textcolor{blue}{0}$
Her er to snittet for $y = 2$, dvs. når $z = f(x,2) = x + 2$:
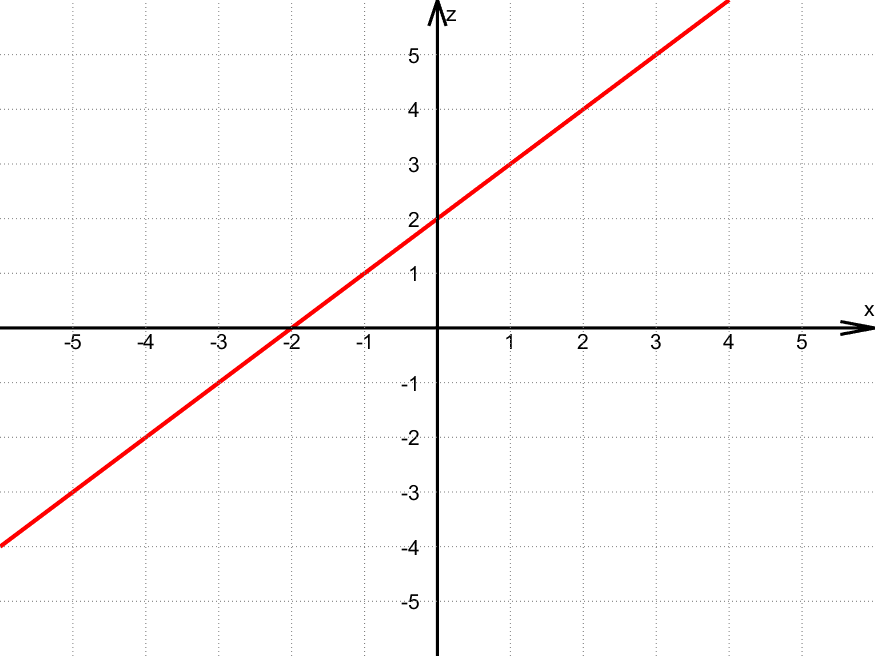
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{2})$ fordi $z = f(\textcolor{red}{0},2) = \textcolor{red}{0} + 2 = \textcolor{blue}{2}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{4})$ fordi $z = f(\textcolor{red}{2},2) = \textcolor{red}{2} + 2 = \textcolor{blue}{4}$
+ Eksempel 2: $f(x,y) = 12 \:-\: x^2 \:-\: 2y^2$
+ Kort video
Nivåkurver:
+ Grafen til $f(x,y) = 12 \:-\: x^2 \:-\: 2y^2$
Grafen til $f(x,y)$ består av alle punkt $(x,y,z)$ som tilfredsstiller $f(x,y) = z$:
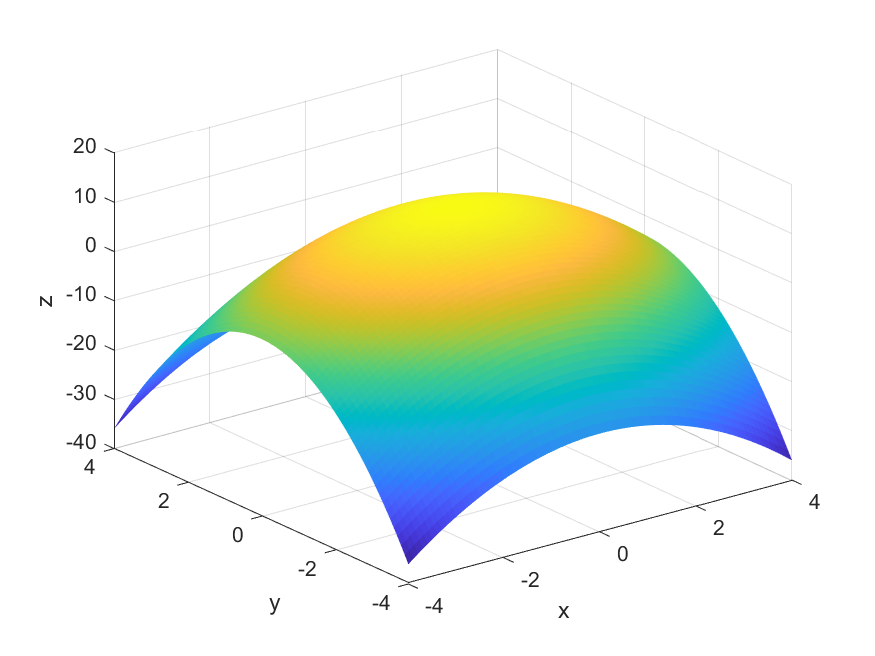
Eksempler på punkt på grafen er:
- $(x,y,z) = (0,0,12)$ fordi $f(0,0) = 12 – 0^2 – 2 \cdot 0^2 = 12$
- $(x,y,z) = (0,2,4)$ fordi $f(0,2) = 12 – 0^2 – 2 \cdot 2^2 = 4$
- $(x,y,z) = (3,2,-5)$ fordi $f(3,2) = 12 – 3^2 – 2 \cdot 2^2 = -5$
+ Nivåkurver til $f(x,y) = 12 \:-\: x^2 \:-\: 2y^2$
Nivåkurvene til $f(x,y)$ er kurver der $f(x,y)$ er konstant. Her er nivåkurvene $f(x,y) = k$ for noen valg av $k$:
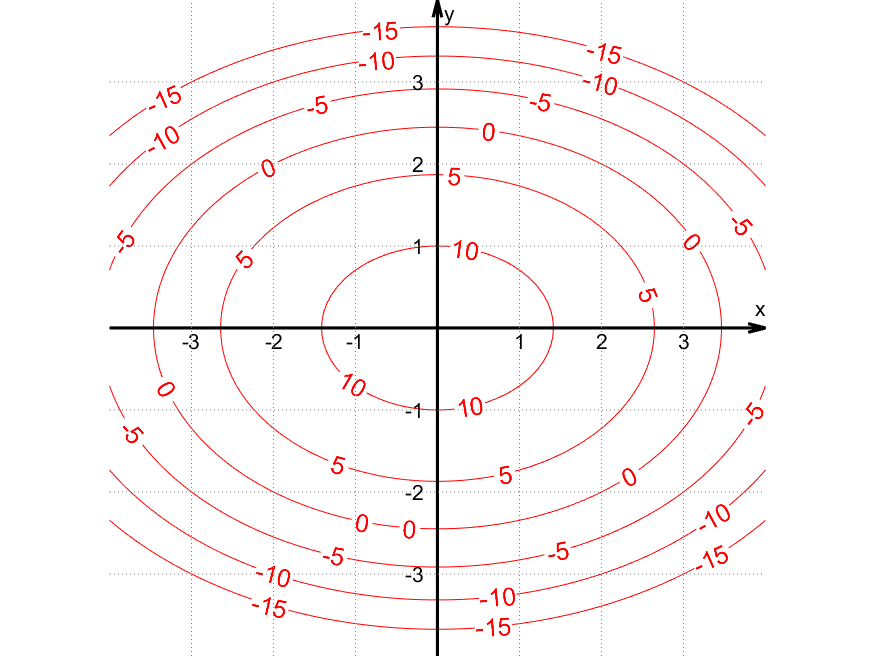
Eksempler på punkt på kurven for $k=\textcolor{red}{10}$:
- $(x,y) = (0,1)$ fordi $f(0,1) = 12 – 0^2 – 2\cdot 1^2 = \textcolor{red}{10}$
- $(x,y) = (0,-1)$ fordi $f(0,-1) = 12 – 0^2 – 2\cdot (-1)^2 = \textcolor{red}{10}$
+ Snitt til $f(x,y) = 12 \:-\: x^2 \:-\: 2y^2$
Et snitt kan tegnes for akkurat den $x$ eller $y$ verdien man ønsker.
Her er to snittet for $y = 0$, dvs. når $z = f(x,0) = x + 0$:
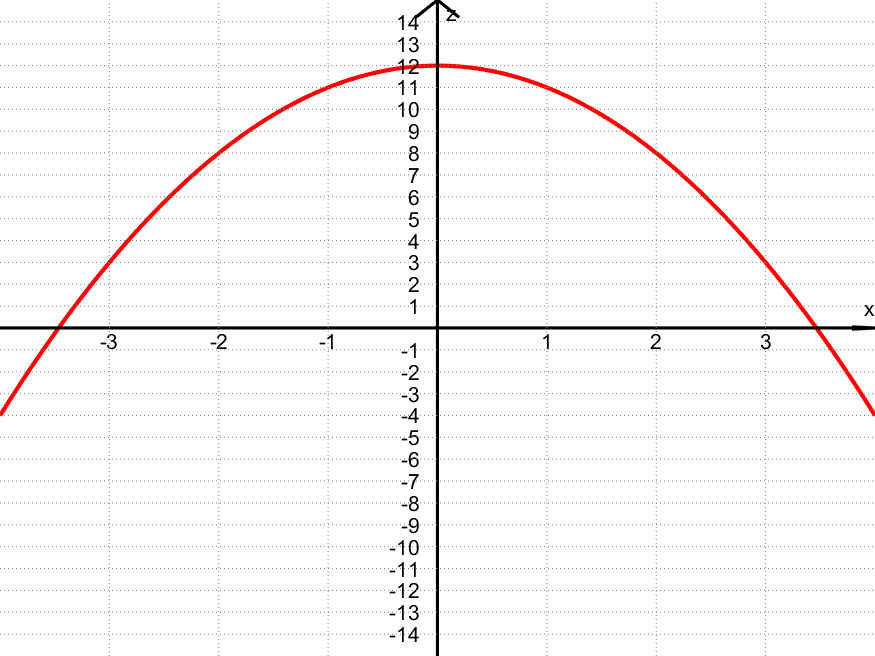
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{12})$ fordi $z = f(\textcolor{red}{0},0) = 12 – \textcolor{red}{0}^2 – 2 \cdot 0^2 = \textcolor{blue}{12}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{8})$ fordi $z = f(\textcolor{red}{2},0) = 12 – \textcolor{red}{2}^2 – 2 \cdot 0^2 = \textcolor{blue}{8}$
Her er to snittet for $y = 2$, dvs. når $z = f(x,2) = x + 2$:
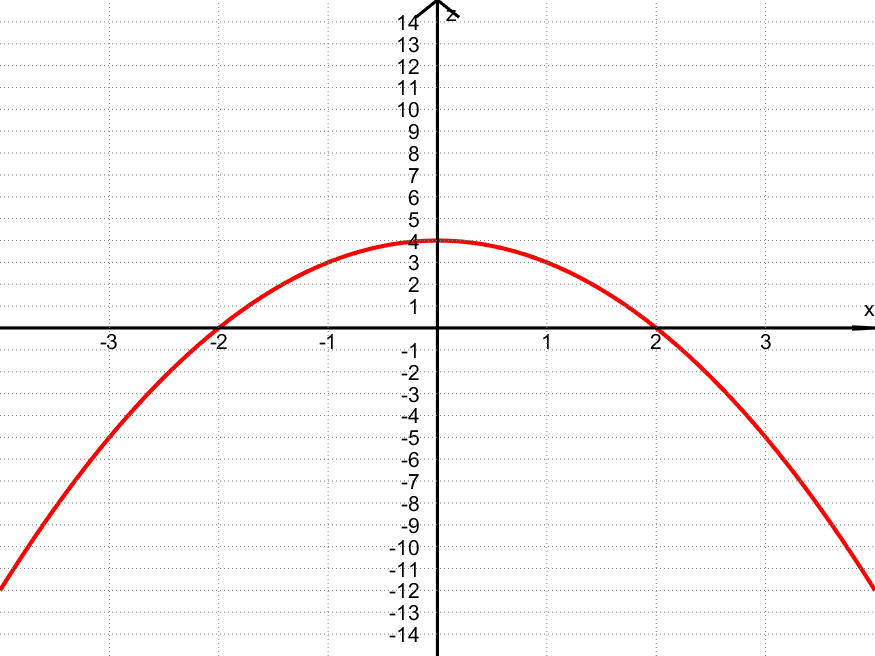
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{4})$ fordi $z = f(\textcolor{red}{0},2) = 12 – \textcolor{red}{0}^2 – 2 \cdot 2^2 = \textcolor{blue}{4}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{0})$ fordi $z = f(\textcolor{red}{2},2) = 12 – \textcolor{red}{2}^2 – 2 \cdot 2^2 = \textcolor{blue}{0}$
+ Eksempel 3: $f(x,y) = x^2 \:-\: y^2$
+ Grafen til $f(x,y) = x^2 \:-\: y^2$
Grafen til $f(x,y)$ består av alle punkt $(x,y,z)$ som tilfredsstiller $f(x,y) = z$:
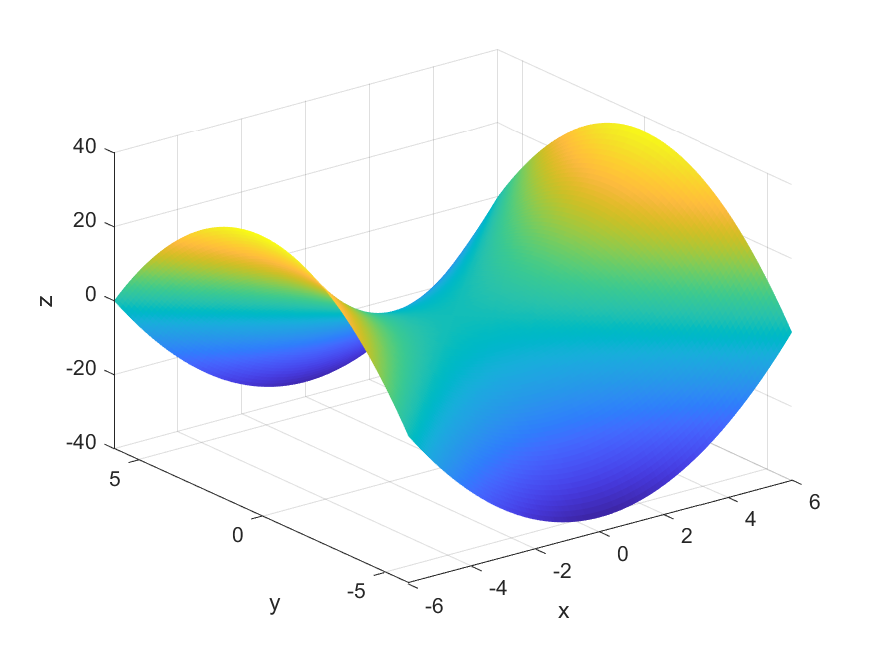
Eksempler på punkt på grafen er:
- $(x,y,z) = (0,0,0)$ fordi $f(0,0) = 0^2 – 0^2 = 0$
- $(x,y,z) = (0,2,-4)$ fordi $f(0,2) = 0^2 – 2^2 = -4$
- $(x,y,z) = (3,2,5)$ fordi $f(3,2) = 3^2 – 2^2 = 5$
+ Nivåkurver til $f(x,y) = x^2 \:-\: y^2$
Nivåkurvene til $f(x,y)$ er kurver der $f(x,y)$ er konstant. Her er nivåkurvene $f(x,y) = k$ for noen valg av $k$:
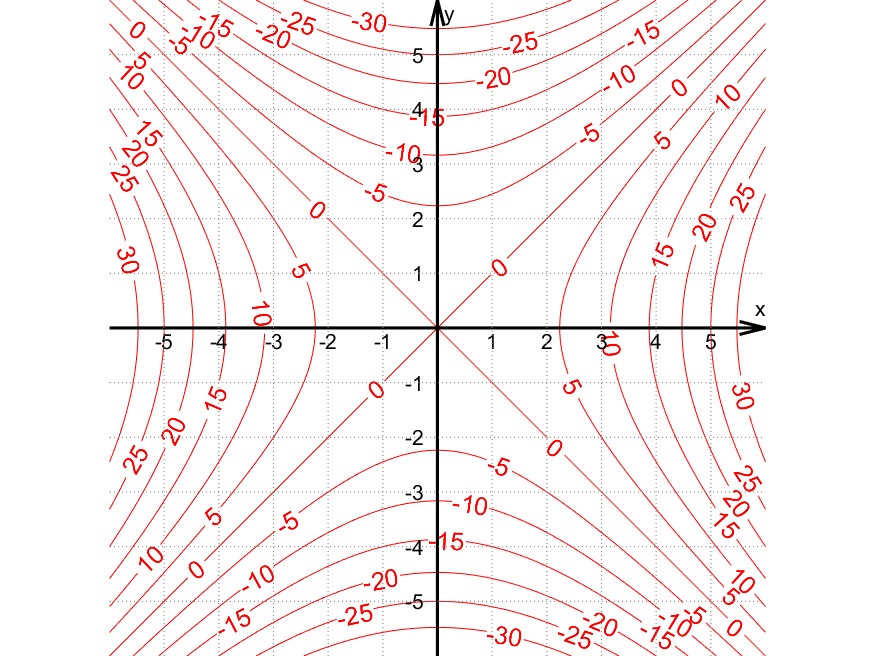
Eksempler på punkt på kurven for $k=\textcolor{red}{0}$:
- $(x,y) = (2,2)$ fordi $f(2,2) = 2^2 – 2^2 = \textcolor{red}{0}$
- $(x,y) = (3,-3)$ fordi $f(3,-3) = 3^2 – (-3)^2 = \textcolor{red}{0}$
+ Snitt til $f(x,y) = x^2 \:-\: y^2$
Et snitt kan tegnes for akkurat den $x$ eller $y$ verdien man ønsker.
Her er to snittet for $y = 0$, dvs. når $z = f(x,0) = x + 0$:
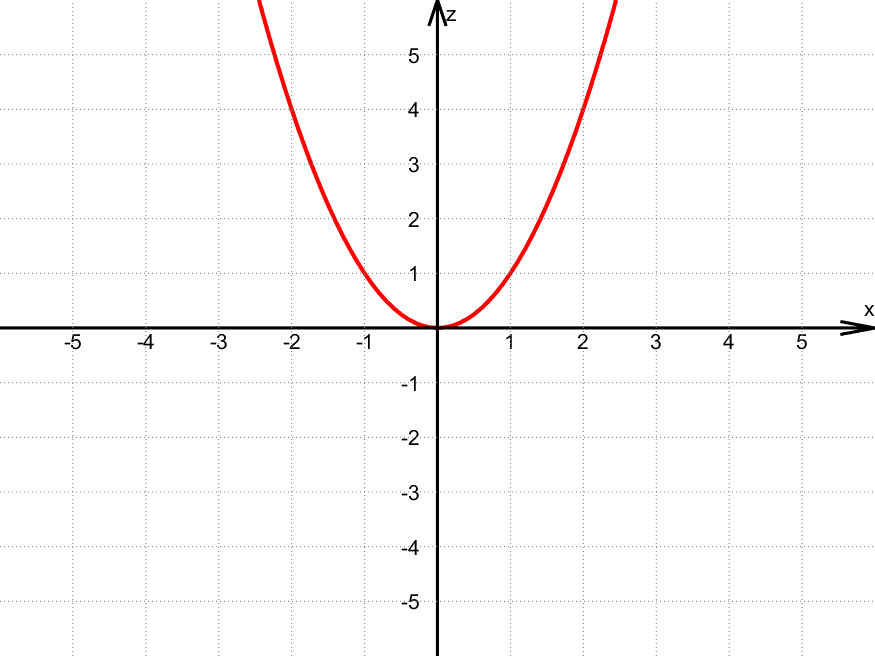
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{12})$ fordi $z = f(\textcolor{red}{0},0) = \textcolor{red}{0}^2 – 0^2 = \textcolor{blue}{0}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{8})$ fordi $z = f(\textcolor{red}{2},0) = \textcolor{red}{2}^2 – 0^2 = \textcolor{blue}{4}$
Her er to snittet for $y = 2$, dvs. når $z = f(x,2) = x + 2$:
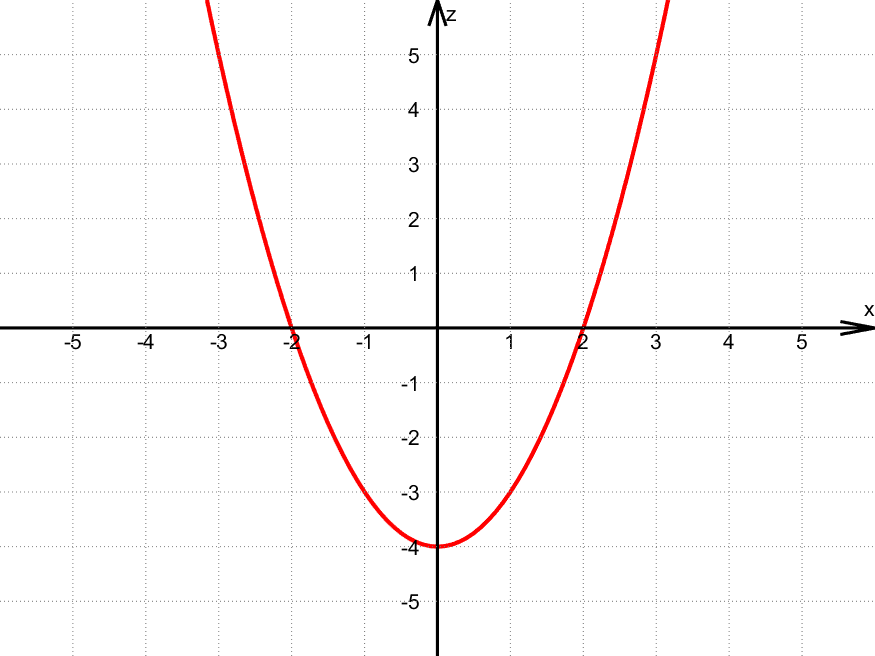
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{4})$ fordi $z = f(\textcolor{red}{0},2) = \textcolor{red}{0}^2 – 2^2 = \textcolor{blue}{-4}$
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{0})$ fordi $z = f(\textcolor{red}{2},2) = \textcolor{red}{2}^2 – 2^2 = \textcolor{blue}{0}$
+ Eksempel 4: $f(x,y) = 3x^2 + 2y^3 \:-\: 6xy$
+ Grafen til $f(x,y) = 3x^2 + 2y^3 \:-\: 6xy$
Grafen til $f(x,y)$ består av alle punkt $(x,y,z)$ som tilfredsstiller $f(x,y) = z$:
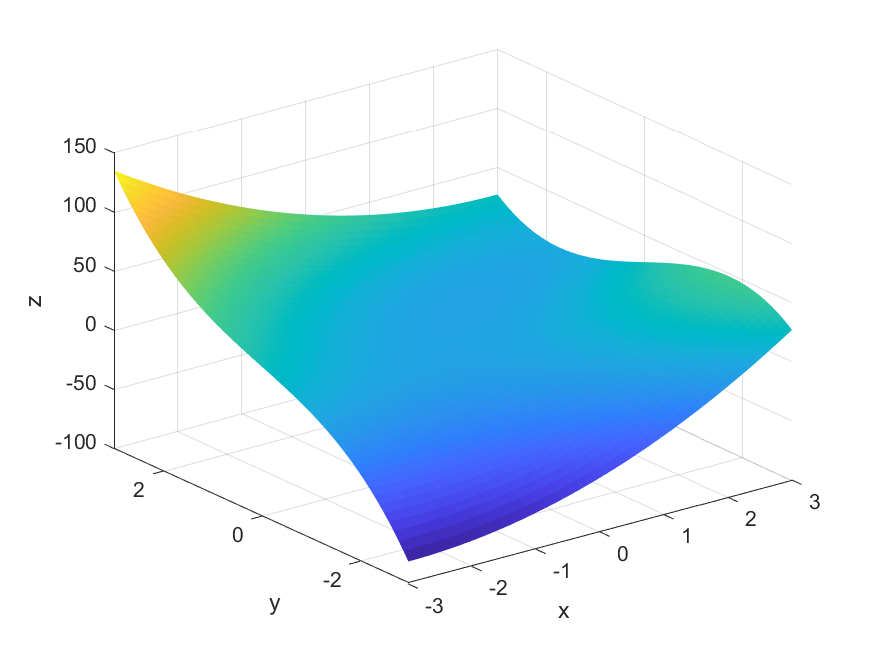
Eksempler på punkt på grafen er:
- $(x,y,z) = (0,0,0)$ fordi $f(0,0) = 3 \cdot 0^2 – 2\cdot 0^3 \:-\: 6 \cdot 0 \cdot 0 = 0$
- $(x,y,z) = (0,2,-16)$ fordi $f(0,2) = 3 \cdot 0^2 – 2\cdot 2^3 \:-\: 6 \cdot 0 \cdot 2 = -16$
- $(x,y,z) = (3,2,-63)$ fordi $f(3,2) = 3 \cdot 3^2 – 2\cdot 3^3 \:-\: 6 \cdot 3 \cdot 2 = -63$
+ Nivåkurver til $f(x,y) = 3x^2 + 2y^3 \:-\: 6xy$
Nivåkurvene til $f(x,y)$ er kurver der $f(x,y)$ er konstant. Her er nivåkurvene $f(x,y) = k$ for noen valg av $k$:
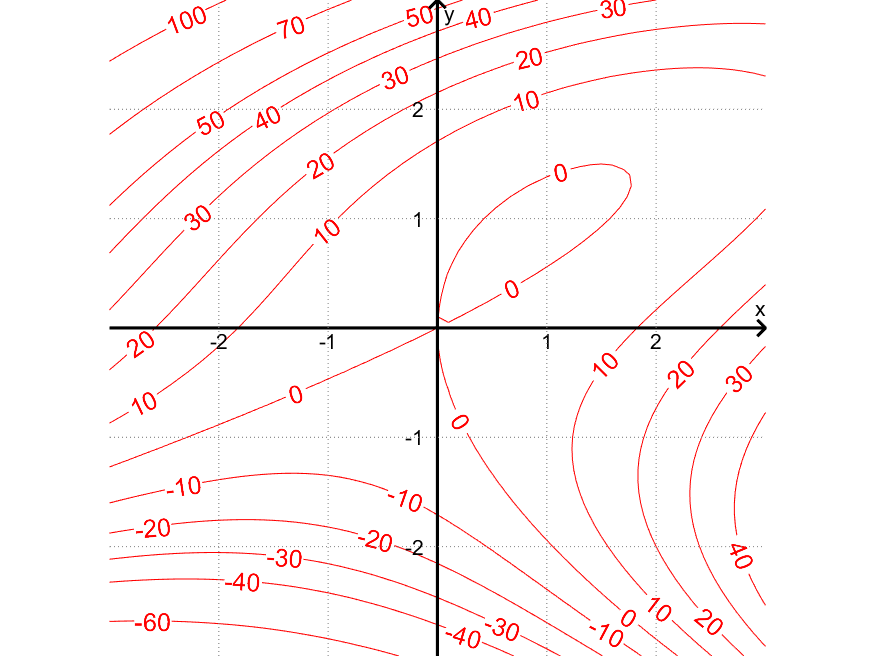
Eksempler på punkt på kurven for $k=\textcolor{red}{0}$:
- $(x,y) = (0,0)$ fordi $f(0,0) = 3 \cdot 0^2 + 2\cdot 0^3 \:-\: 6 \cdot 0 \cdot 0 = \textcolor{red}{0}$
- $(x,y) = (1 + \sqrt{\frac{5}{3}},1)$ fordi $f(1 + \sqrt{\frac{5}{3}},-3) = 3 \cdot \left( 1 + \sqrt{\frac{5}{3}} \right)^2 + 2\cdot 1^3 \:-\: 6 \cdot \left( 1 + \sqrt{\frac{5}{3}} \right) \cdot 1 = \textcolor{red}{0}$
+ Snitt til $f(x,y) = 3x^2 + 2y^3 \:-\: 6xy$
Et snitt kan tegnes for akkurat den $x$ eller $y$ verdien man ønsker.
Her er to snittet for $y = 0$, dvs. når $z = f(x,0) = 3x^2$:
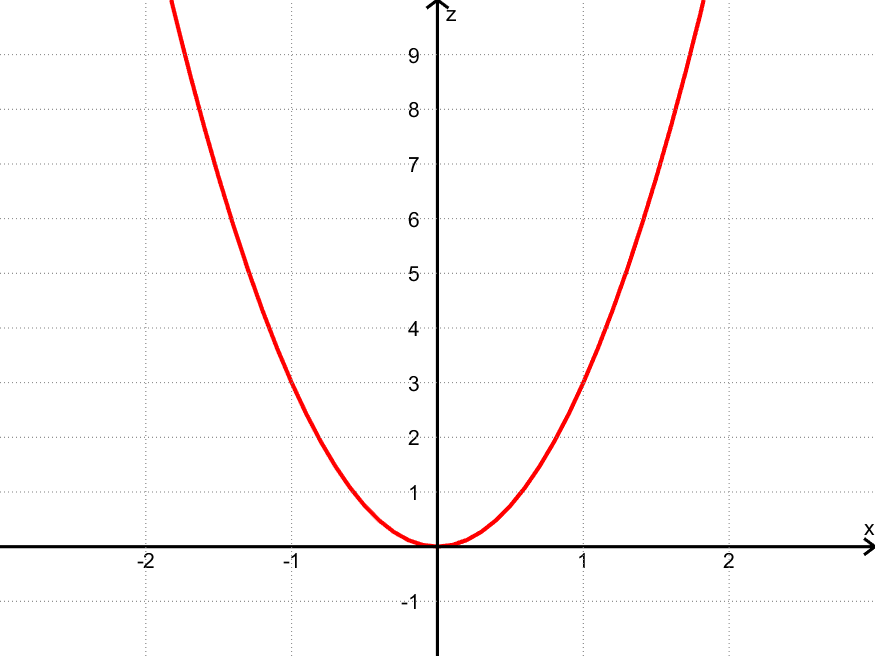
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{0})$ fordi $z = f(\textcolor{red}{0},0) = 3 \cdot \textcolor{red}{0}^2 = \textcolor{blue}{0}$
- $(x,z) = (\textcolor{red}{1},\textcolor{blue}{3})$ fordi $z = f(\textcolor{red}{1},0) = 3 \cdot \textcolor{red}{1}^2 = \textcolor{blue}{3}$
Her er to snittet for $y = 2$, dvs. når $z = f(x,2) = 3x^2 + 16 \:-\:12x$:
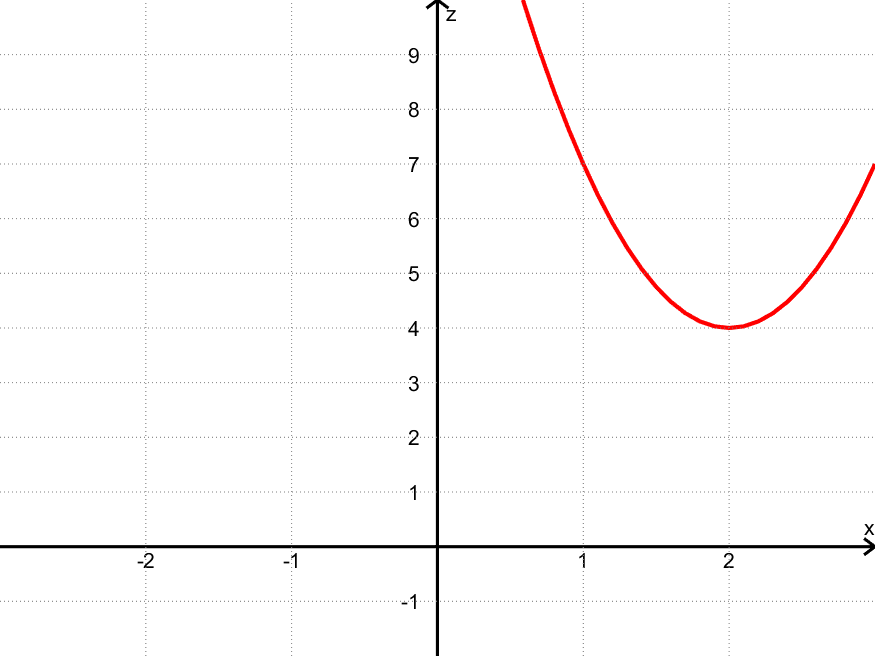
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{2},\textcolor{blue}{4})$ fordi $z = f(\textcolor{red}{2},2) = 3 \cdot \textcolor{red}{2}^2 + 16 \:-\: 12 \cdot \textcolor{red}{2} = \textcolor{blue}{4}$
- $(x,z) = (\textcolor{red}{1},\textcolor{blue}{7})$ fordi $z = f(\textcolor{red}{1},2) = 3 \cdot \textcolor{red}{1}^2 + 16 \:-\_ 12 \cdot \textcolor{red}{1} = \textcolor{blue}{7}$
+ Eksempel 5: $f(x,y) = x^2 \:-\: 2x + 2y^2 \:-\: 8y + 3$
+ Grafen til $f(x,y) = x^2 \:-\: 2x + 2y^2 \:-\: 8y + 3$
Grafen til $f(x,y)$ består av alle punkt $(x,y,z)$ som tilfredsstiller $f(x,y) = z$:
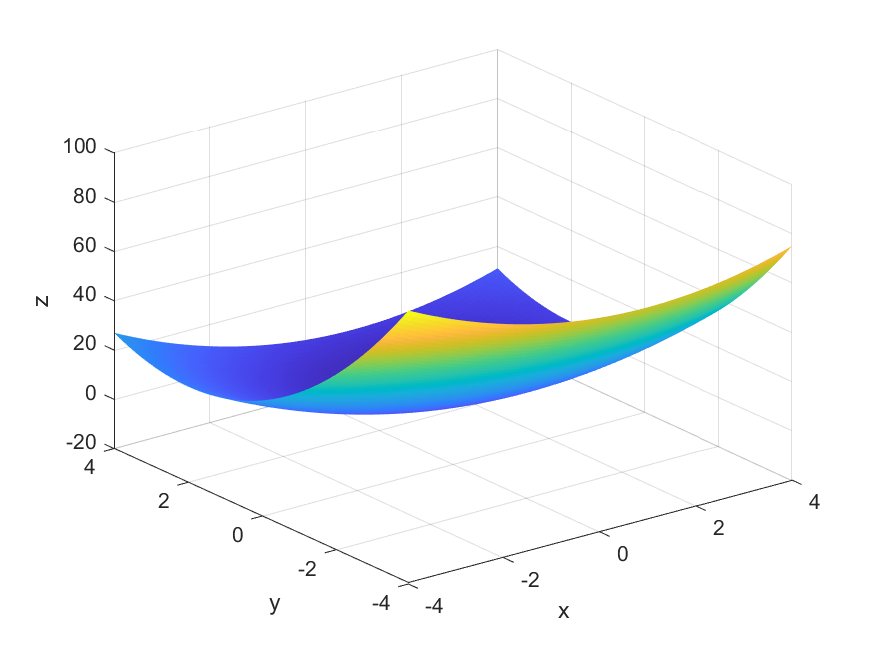
Eksempler på punkt på grafen er:
- $(x,y,z) = (0,0,3)$ fordi $f(0,0) = 0^2 \:-\: 2\cdot 0 + 2 \cdot 0^2 \:-\: 8 \cdot 0 + 3 = 3$
- $(x,y,z) = (1,2,-6)$ fordi $f(0,2) = 1^2 \:-\: 2\cdot 1 + 2 \cdot 2^2 \:-\: 8 \cdot 2 + 3 = -6$
- $(x,y,z) = (2,1,)$ fordi $f(2,1) = 2^2 \:-\: 2\cdot 2 + 2 \cdot 1^2 \:-\: 8 \cdot 1 + 3 = -3$
+ Nivåkurver til $f(x,y) = x^2 \:-\: 2x + 2y^2 \:-\: 8y + 3$
Nivåkurvene til $f(x,y)$ er kurver der $f(x,y)$ er konstant. Her er nivåkurvene $f(x,y) = k$ for noen valg av $k$:
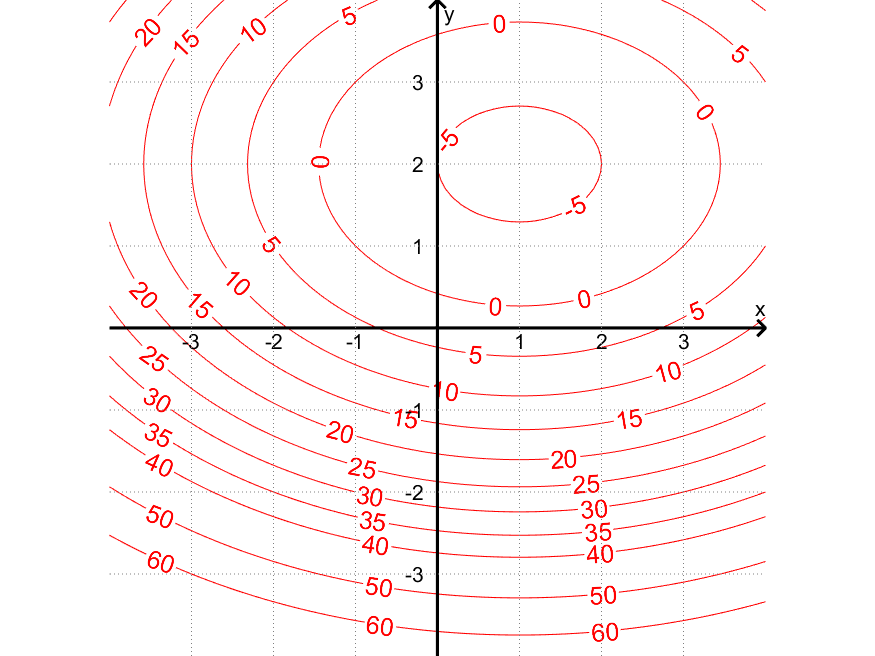
Eksempler på punkt på kurven for $k=\textcolor{red}{-5}$:
- $(x,y) = (0,2)$ fordi $f(0,2) = 0^2 – 2\cdot 0 + 2 \cdot 2^2 \:-\: 8 \cdot 2 + 3 = \textcolor{red}{-5}$
- $(x,y) = (2,2)$ fordi $f(2,2) = 2^2 – 2\cdot 2 + 2 \cdot 2^2 \:-\: 8 \cdot 2 + 3 = \textcolor{red}{-5}$
+ Snitt til $f(x,y) = x^2 \:-\: 2x + 2y^2 \:-\: 8y – 5$
Et snitt kan tegnes for akkurat den $x$ eller $y$ verdien man ønsker.
Her er to snittet for $y = 0$, dvs. når $z = f(x,0) = x^2 \:-\: 2x + 3$:
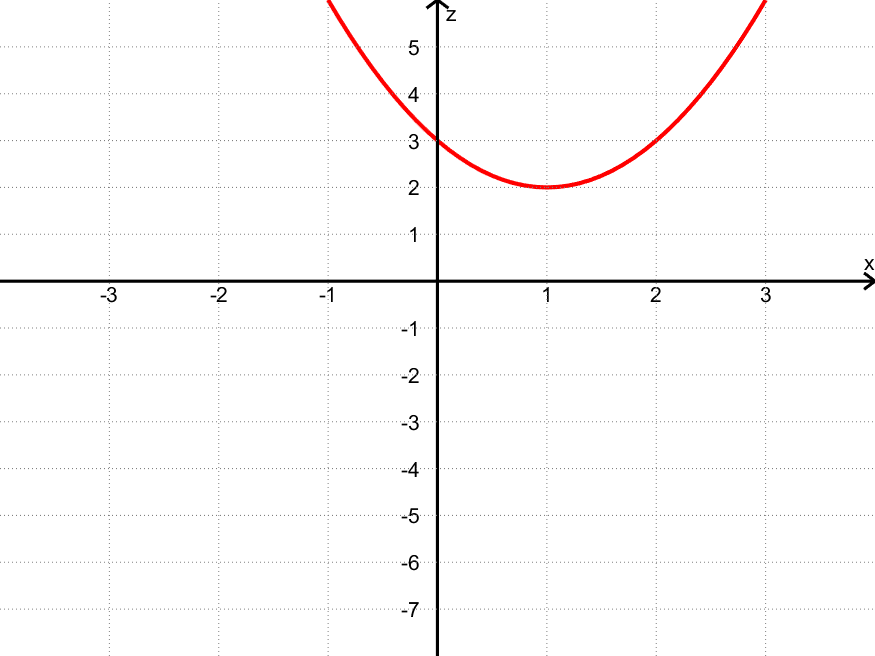
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{3})$ fordi $z = f(\textcolor{red}{0},0) = \textcolor{red}{0}^2 \:-\: 2\cdot \textcolor{red}{0} + 3 = \textcolor{blue}{3}$
- $(x,z) = (\textcolor{red}{1},\textcolor{blue}{2})$ fordi $z = f(\textcolor{red}{1},0) = \textcolor{red}{1}^2 \:-\: 2\cdot \textcolor{red}{1} + 3 = \textcolor{blue}{2}$
Her er to snittet for $y = 2$, dvs. når $z = f(x,2) =x^2 \:-\: 2x – 5 $:
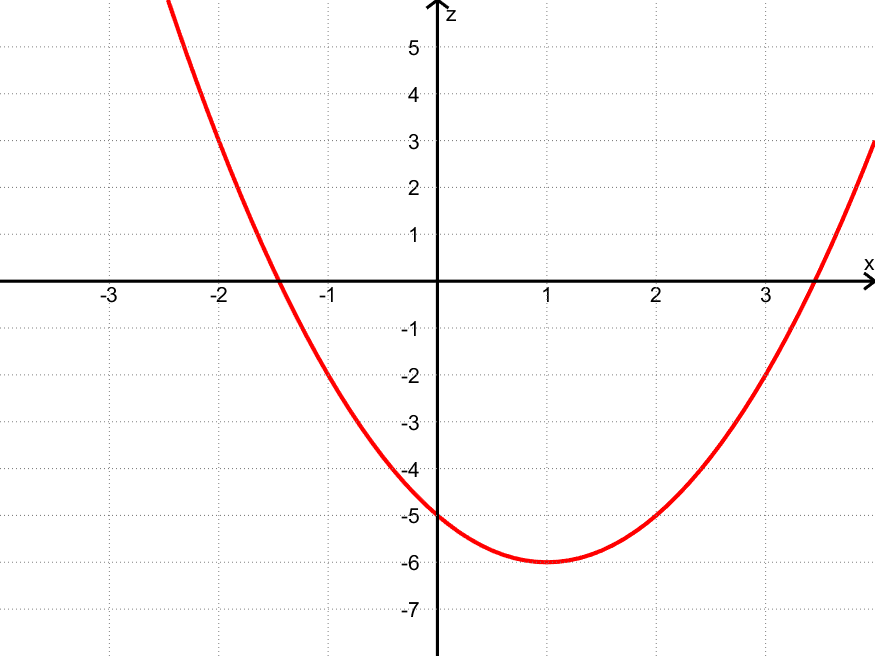
Eksempler på punkt på kurven:
- $(x,z) = (\textcolor{red}{0},\textcolor{blue}{-5})$ fordi $z = f(\textcolor{red}{0},-5) = \textcolor{red}{0}^2 \:-\: 2\cdot \textcolor{red}{0} \:-\: 5 = \textcolor{blue}{3}$
- $(x,z) = (\textcolor{red}{1},\textcolor{blue}{7})$ fordi $z = f(\textcolor{red}{0},0) = \textcolor{red}{1}^2 \:-\: 2\cdot \textcolor{red}{1} \:-\: 5 = \textcolor{blue}{-6}$
